분할 정복 알고리즘의 하나, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법
Goal
- 퀵 정렬(quick sort) 알고리즘을 이해한다.
- 퀵 정렬(quick sort) 알고리즘을 c언어로 구현한다.
- 퀵 정렬(quick sort) 알고리즘의 특징
- 퀵 정렬(quick sort) 알고리즘의 시간복잡도를 이해한다.
들어가기 전
- 오름차순을 기준으로 정렬한다.
퀵 정렬(quick sort) 알고리즘의 개념 요약
- ‘찰스 앤터니 리처드 호어(Charles Antony Richard Hoare)’가 개발한 정렬 알고리즘
- 퀵 정렬은 불안정 정렬 에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬 에 속한다.
- 분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법
- 합병 정렬(merge sort)과 달리 퀵 정렬은 리스트를 비균등하게 분할한다.
- 분할 정복(divide and conquer) 방법
- 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
- 분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
- 과정 설명
- 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
- 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
- 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
- 리스트의 크기가 0이나 1이 될 때까지 반복한다.
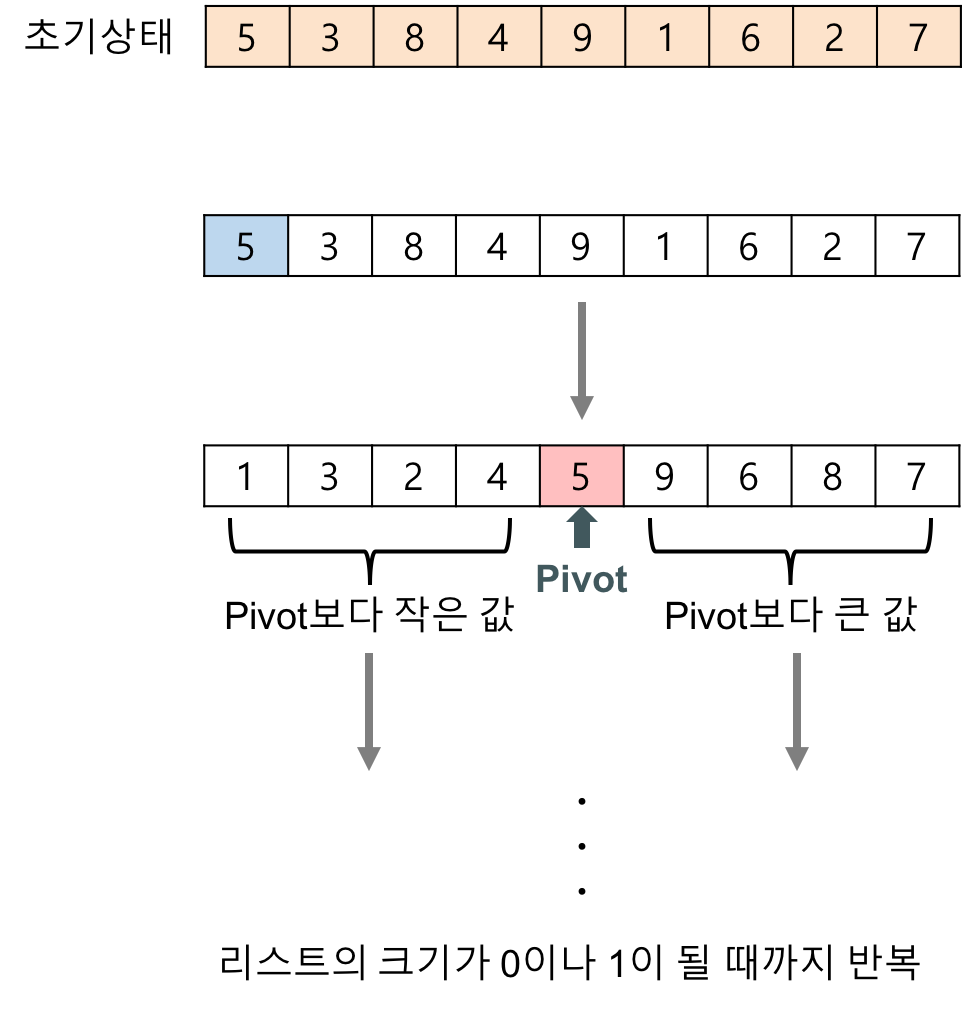
퀵 정렬(quick sort) 알고리즘의 구체적인 개념
- 하나의 리스트를 피벗(pivot)을 기준으로 두 개의 비균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
- 퀵 정렬은 다음의 단계들로 이루어진다.
- 분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
- 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
- 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
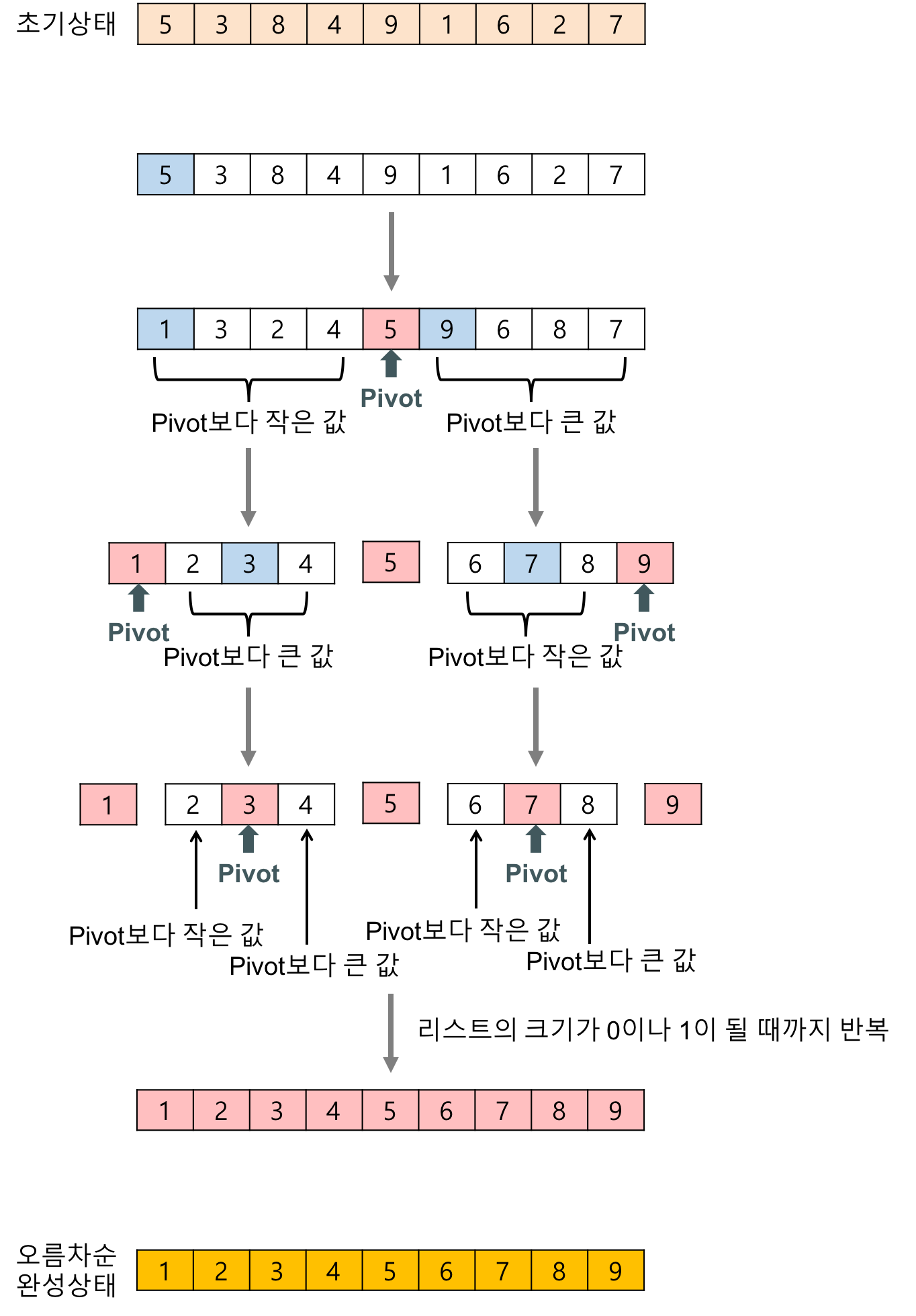
퀵 정렬(quick sort) 알고리즘의 예제
- 배열에 5, 3, 8, 4, 9, 1, 6, 2, 7이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
- 퀵 정렬에서 피벗을 기준으로 두 개의 리스트로 나누는 과정(c언어 코드의 partition 함수의 내용)
-
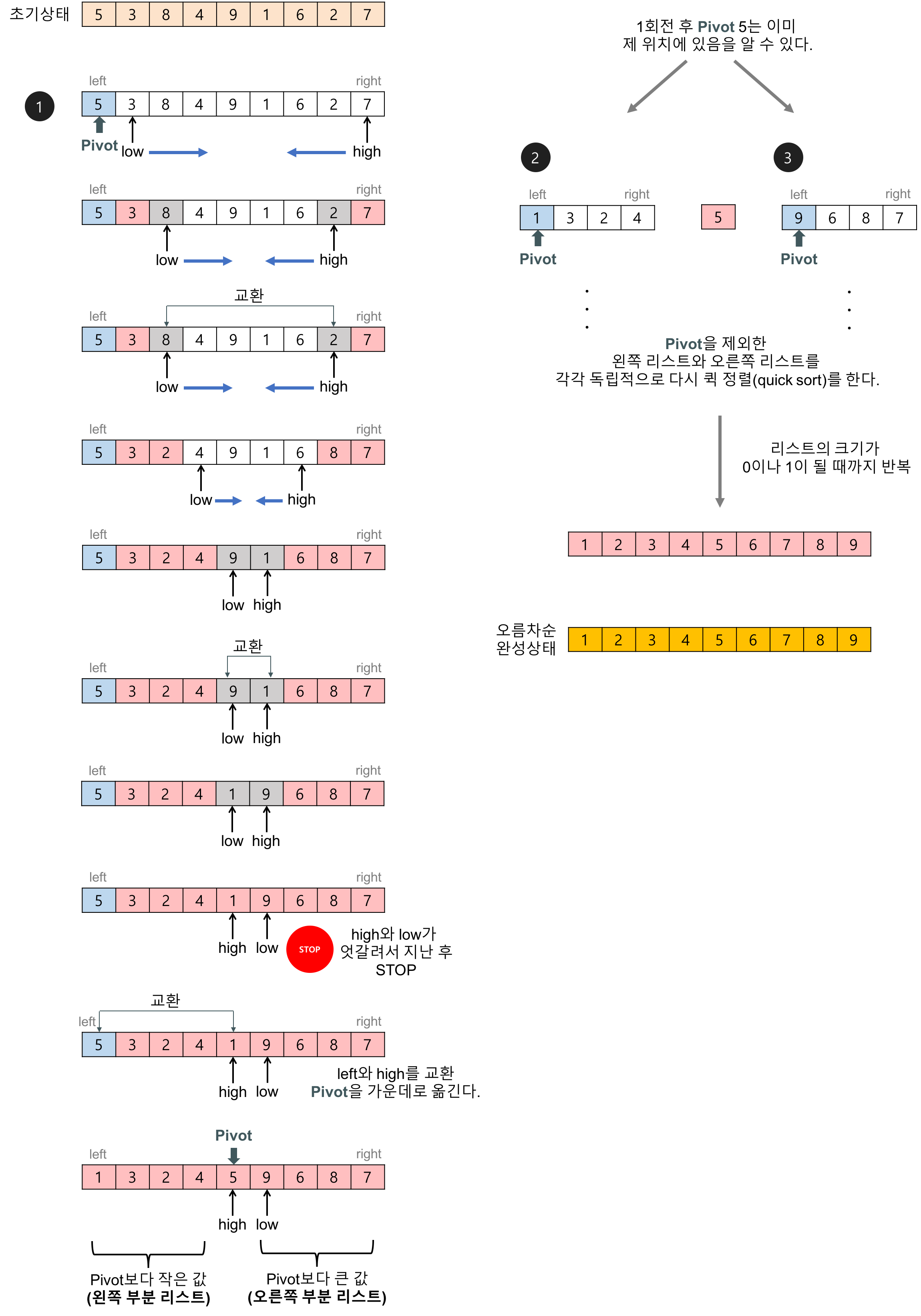
- 피벗 값을 입력 리스트의 첫 번째 데이터로 하자. (다른 임의의 값이어도 상관없다.)
- 2개의 인덱스 변수(low, high)를 이용해서 리스트를 두 개의 부분 리스트로 나눈다.
- 1회전: 피벗이 5인 경우,
- low는 왼쪽에서 오른쪽으로 탐색해가다가 피벗보다 큰 데이터(8)을 찾으면 멈춘다.
- high는 오른쪽에서 왼쪽으로 탐색해가다가 피벗보다 작은 데이터(2)를 찾으면 멈춘다.
- low와 high가 가리키는 두 데이터를 서로 교환한다.
- 이 탐색-교환 과정은 low와 high가 엇갈릴 때까지 반복한다.
- 2회전: 피벗(1회전의 왼쪽 부분리스트의 첫 번째 데이터)이 1인 경우,
- 위와 동일한 방법으로 반복한다.
- 3회전: 피벗(1회전의 오른쪽 부분리스트의 첫 번째 데이터)이 9인 경우,
- 위와 동일한 방법으로 반복한다.
퀵 정렬(quick sort) c언어 코드
# include <stdio.h>
# define MAX_SIZE 9
# define SWAP(x, y, temp) ( (temp)=(x), (x)=(y), (y)=(temp) )
// 1. 피벗을 기준으로 2개의 부분 리스트로 나눈다.
// 2. 피벗보다 작은 값은 모두 왼쪽 부분 리스트로, 큰 값은 오른쪽 부분 리스트로 옮긴다.
/* 2개의 비균등 배열 list[left...pivot-1]와 list[pivot+1...right]의 합병 과정 */
/* (실제로 숫자들이 정렬되는 과정) */
int partition(int list[], int left, int right){
int pivot, temp;
int low, high;
low = left;
high = right + 1;
pivot = list[left]; // 정렬할 리스트의 가장 왼쪽 데이터를 피벗으로 선택(임의의 값을 피벗으로 선택)
/* low와 high가 교차할 때까지 반복(low<high) */
do{
/* list[low]가 피벗보다 작으면 계속 low를 증가 */
do {
low++; // low는 left+1 에서 시작
} while (low<=right && list[low]<pivot);
/* list[high]가 피벗보다 크면 계속 high를 감소 */
do {
high--; //high는 right 에서 시작
} while (high>=left && list[high]>pivot);
// 만약 low와 high가 교차하지 않았으면 list[low]를 list[high] 교환
if(low<high){
SWAP(list[low], list[high], temp);
}
} while (low<high);
// low와 high가 교차했으면 반복문을 빠져나와 list[left]와 list[high]를 교환
SWAP(list[left], list[high], temp);
// 피벗의 위치인 high를 반환
return high;
}
// 퀵 정렬
void quick_sort(int list[], int left, int right){
/* 정렬할 범위가 2개 이상의 데이터이면(리스트의 크기가 0이나 1이 아니면) */
if(left<right){
// partition 함수를 호출하여 피벗을 기준으로 리스트를 비균등 분할 -분할(Divide)
int q = partition(list, left, right); // q: 피벗의 위치
// 피벗은 제외한 2개의 부분 리스트를 대상으로 순환 호출
quick_sort(list, left, q-1); // (left ~ 피벗 바로 앞) 앞쪽 부분 리스트 정렬 -정복(Conquer)
quick_sort(list, q+1, right); // (피벗 바로 뒤 ~ right) 뒤쪽 부분 리스트 정렬 -정복(Conquer)
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {5, 3, 8, 4, 9, 1, 6, 2, 7};
// 퀵 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 8)
quick_sort(list, 0, n-1);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
퀵 정렬(quick sort) 알고리즘의 특징
- 장점
- 속도가 빠르다.
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.
- 퀵 정렬은 O(log n)만큼의 메모리를 필요로 한다.
- 속도가 빠르다.
- 단점
- 정렬된 리스트에 대해서는 퀵 정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
- 퀵 정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
- EX) 리스트 내의 몇 개의 데이터 중에서 크기순으로 중간 값(medium)을 피벗으로 선택한다.
퀵 정렬(quick sort)의 시간복잡도
- 최선의 경우
- 비교 횟수
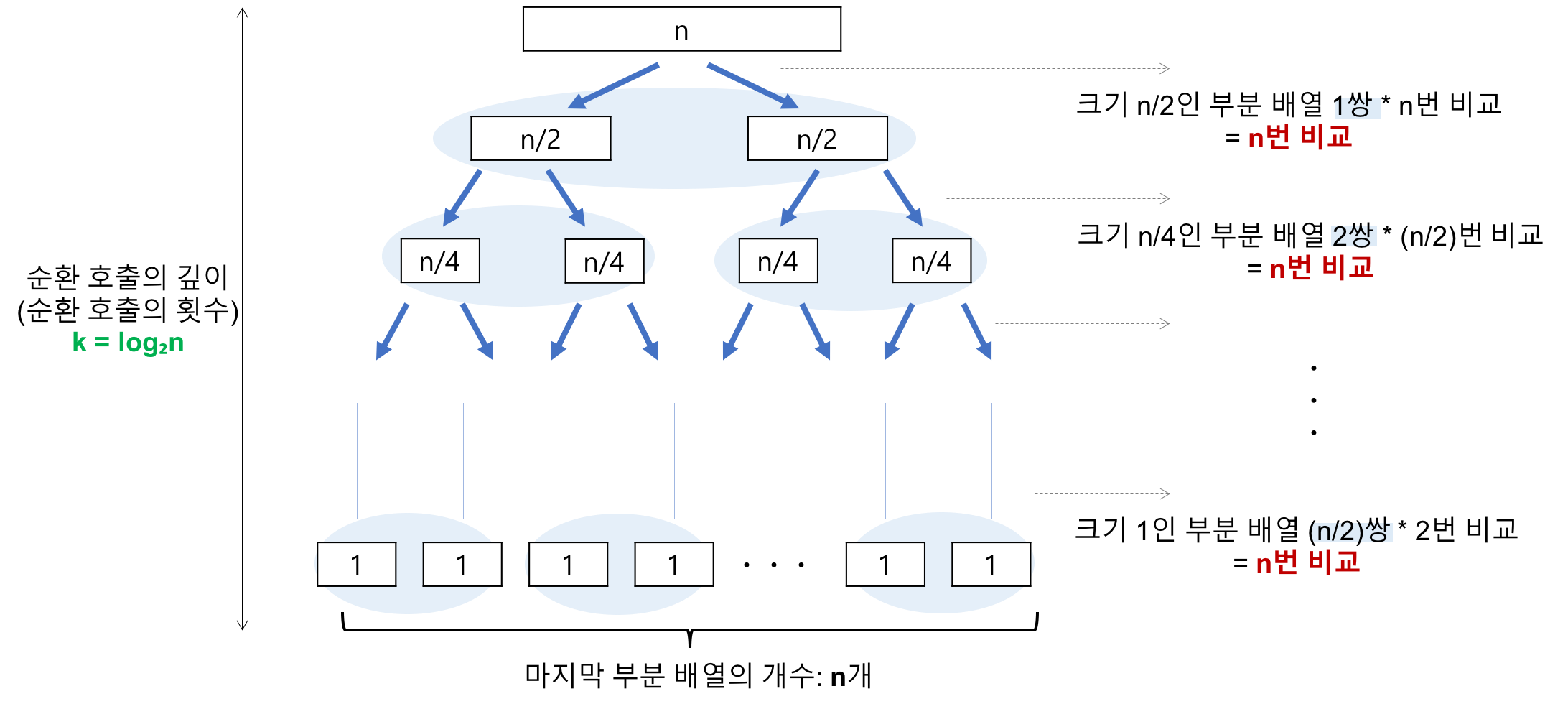
- 순환 호출의 깊이
- 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
- k=log₂n
- 각 순환 호출 단계의 비교 연산
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
- 평균 n번
- 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n
- 이동 횟수
- 비교 횟수보다 적으므로 무시할 수 있다.
- 최선의 경우 T(n) = O(nlog₂n)
- 비교 횟수
- 최악의 경우
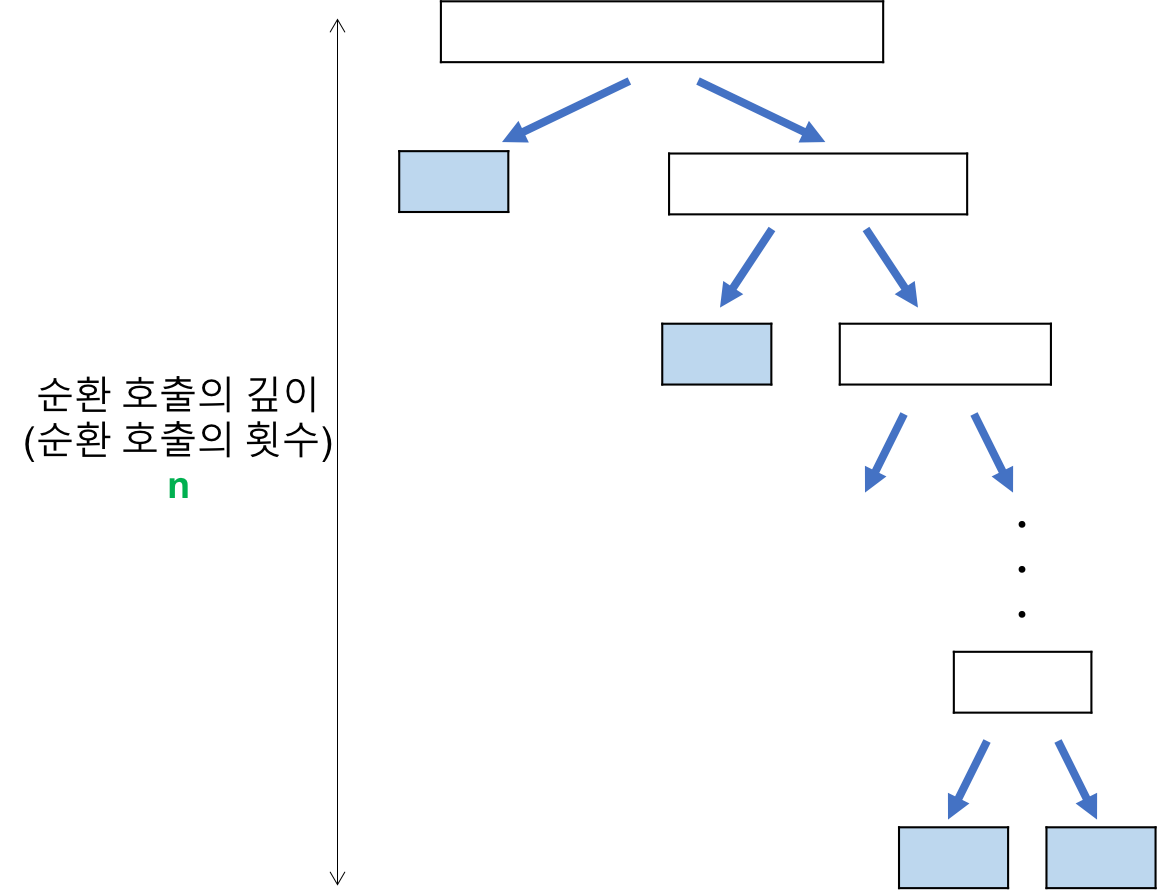
- 리스트가 계속 불균형하게 나누어지는 경우 (특히, 이미 정렬된 리스트에 대하여 퀵 정렬을 실행하는 경우)
- 비교 횟수
- 순환 호출의 깊이
- 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n임을 알 수 있다.
- n
- 각 순환 호출 단계의 비교 연산
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
- 평균 n번
- 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2
- 순환 호출의 깊이
- 이동 횟수
- 비교 횟수보다 적으므로 무시할 수 있다.
- 최악의 경우 T(n) = O(n^2)
- 평균
- 평균 T(n) = O(nlog₂n)
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 퀵 정렬이 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문이다.
정렬 알고리즘 시간복잡도 비교

- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
관련된 Post
- 선택 정렬(selection sort): 선택 정렬(selection sort) 을 참고하시기 바랍니다.
- 삽입 정렬(insertion sort): 삽입 정렬(insertion sort) 을 참고하시기 바랍니다.
- 버블 정렬(bubble sort): 버블 정렬(bubble sort) 을 참고하시기 바랍니다.
- 셸 정렬(shell sort): 셸 정렬(shell sort) 을 참고하시기 바랍니다.
- 합병 정렬(merge sort): 합병 정렬(merge sort) 을 참고하시기 바랍니다.
- 힙 정렬(heap sort): 힙 정렬(heap sort) 을 참고하시기 바랍니다.


