분할 정복 알고리즘의 하나
Goal
- 합병 정렬(merge sort) 알고리즘을 이해한다.
- 합병 정렬(merge sort) 알고리즘을 c언어로 구현한다.
- 합병 정렬(merge sort) 알고리즘의 특징
- 합병 정렬(merge sort) 알고리즘의 시간복잡도를 이해한다.
들어가기 전
- 오름차순을 기준으로 정렬한다.
합병 정렬(merge sort) 알고리즘의 개념 요약
- ‘존 폰 노이만(John von Neumann)’이라는 사람이 제안한 방법
- 일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬 에 속하며, 분할 정복 알고리즘의 하나 이다.
- 분할 정복(divide and conquer) 방법
- 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
- 분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
- 분할 정복(divide and conquer) 방법
- 과정 설명
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
- 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
합병 정렬(merge sort) 알고리즘의 구체적인 개념
- 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
- 합병 정렬은 다음의 단계들로 이루어진다.
- 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
- 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
- 합병 정렬의 과정
- 추가적인 리스트가 필요하다.
- 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용한다.
- 합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계 이다.
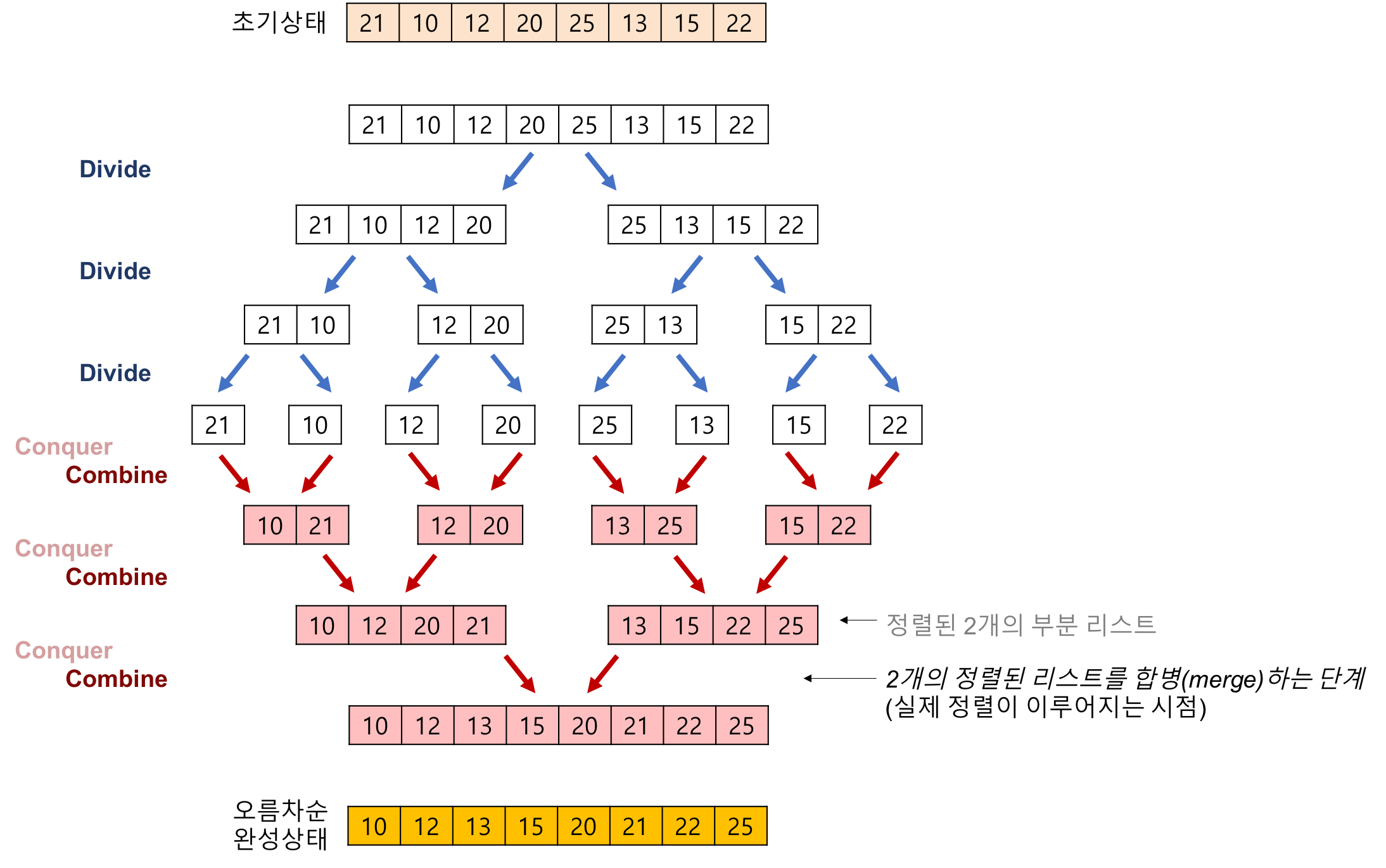
합병 정렬(merge sort) 알고리즘의 예제
- 배열에 27, 10, 12, 20, 25, 13, 15, 22이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
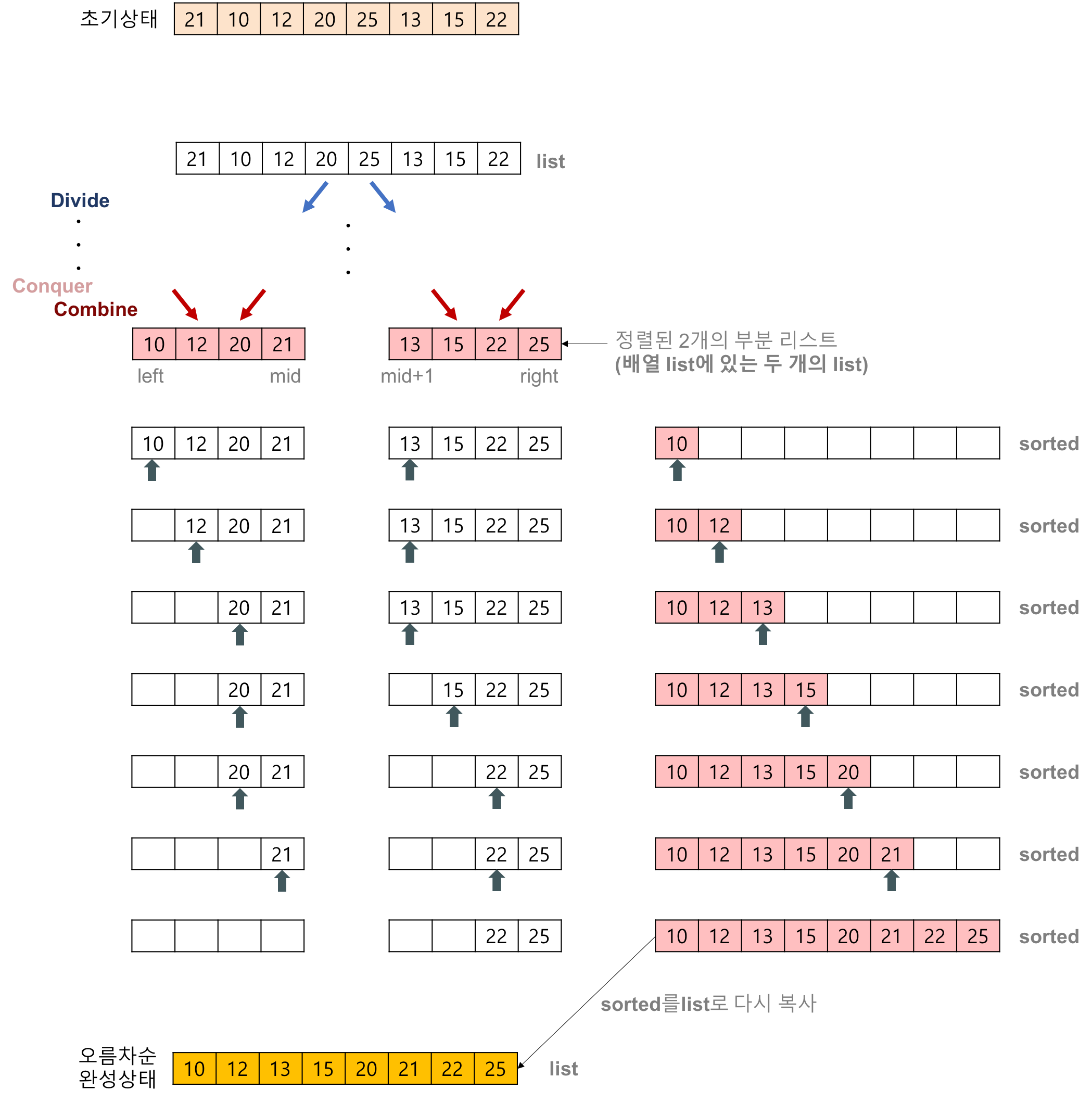
- 2개의 정렬된 리스트를 합병(merge)하는 과정
- 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮긴다.
- 둘 중에서 하나가 끝날 때까지 이 과정을 되풀이한다.
- 만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사한다.
- 새로운 리스트(sorted)를 원래의 리스트(list)로 옮긴다.
합병 정렬(merge sort) c언어 코드
# include <stdio.h>
# define MAX_SIZE 8
int sorted[MAX_SIZE] // 추가적인 공간이 필요
// i: 정렬된 왼쪽 리스트에 대한 인덱스
// j: 정렬된 오른쪽 리스트에 대한 인덱스
// k: 정렬될 리스트에 대한 인덱스
/* 2개의 인접한 배열 list[left...mid]와 list[mid+1...right]의 합병 과정 */
/* (실제로 숫자들이 정렬되는 과정) */
void merge(int list[], int left, int mid, int right){
int i, j, k, l;
i = left;
j = mid+1;
k = left;
/* 분할 정렬된 list의 합병 */
while(i<=mid && j<=right){
if(list[i]<=list[j])
sorted[k++] = list[i++];
else
sorted[k++] = list[j++];
}
// 남아 있는 값들을 일괄 복사
if(i>mid){
for(l=j; l<=right; l++)
sorted[k++] = list[l];
}
// 남아 있는 값들을 일괄 복사
else{
for(l=i; l<=mid; l++)
sorted[k++] = list[l];
}
// 배열 sorted[](임시 배열)의 리스트를 배열 list[]로 재복사
for(l=left; l<=right; l++){
list[l] = sorted[l];
}
}
// 합병 정렬
void merge_sort(int list[], int left, int right){
int mid;
if(left<right){
mid = (left+right)/2 // 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
merge_sort(list, left, mid); // 앞쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, mid+1, right); // 뒤쪽 부분 리스트 정렬 -정복(Conquer)
merge(list, left, mid, right); // 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {21, 10, 12, 20, 25, 13, 15, 22};
// 합병 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 7)
merge_sort(list, 0, n-1);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
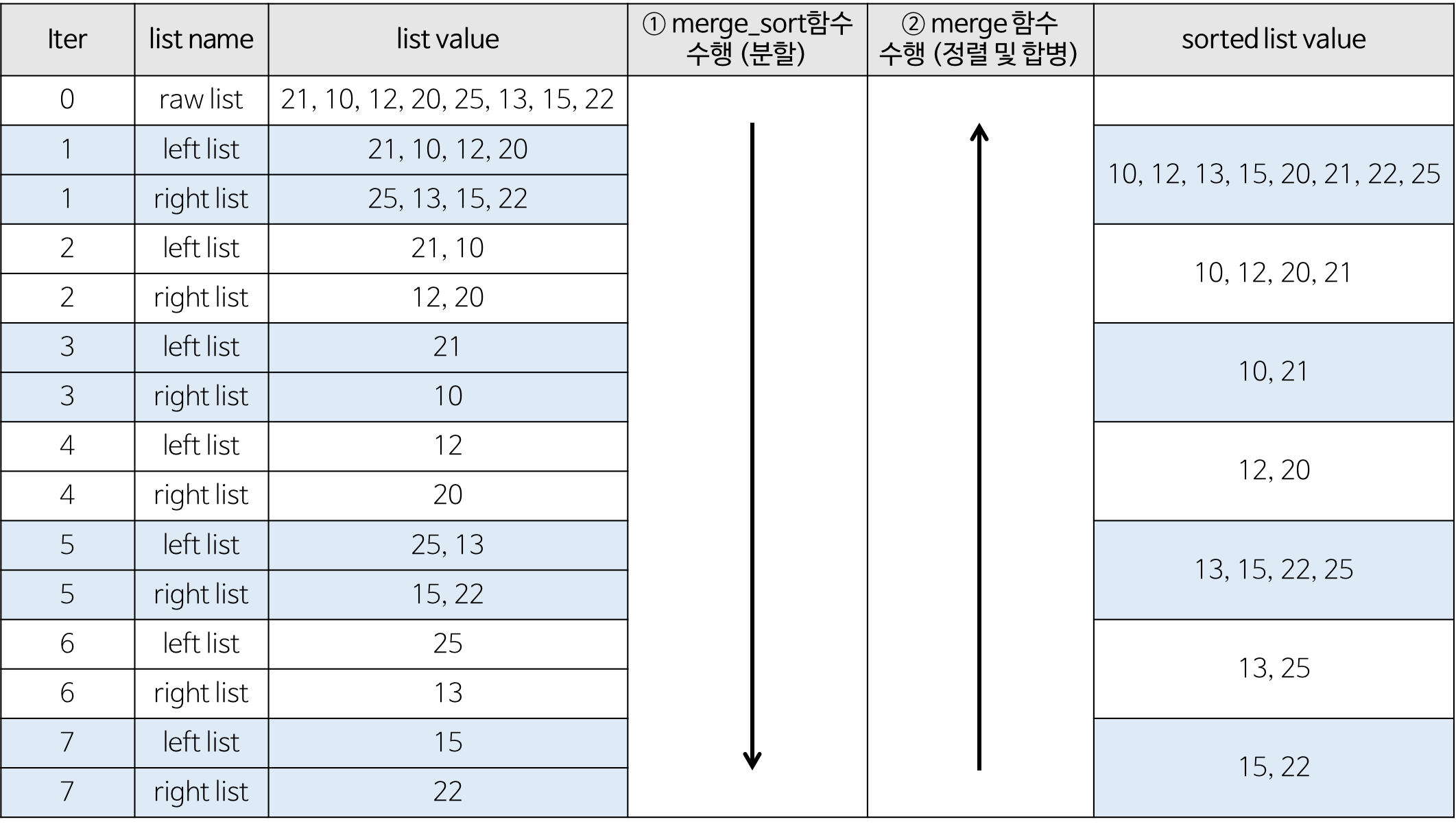
- c언어 코드의 과정
합병 정렬(merge sort) 알고리즘의 특징
- 단점
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.
- 제자리 정렬(in-place sorting)이 아니다.
- 레크드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.
- 장점
- 안정적인 정렬 방법
- 데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (O(nlog₂n)로 동일)
- 만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
- 제자리 정렬(in-place sorting)로 구현할 수 있다.
- 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.
- 안정적인 정렬 방법
합병 정렬(merge sort)의 시간복잡도
시간복잡도를 계산한다면
- 분할 단계
- 비교 연산과 이동 연산이 수행되지 않는다.
- 합병 단계
- 비교 횟수
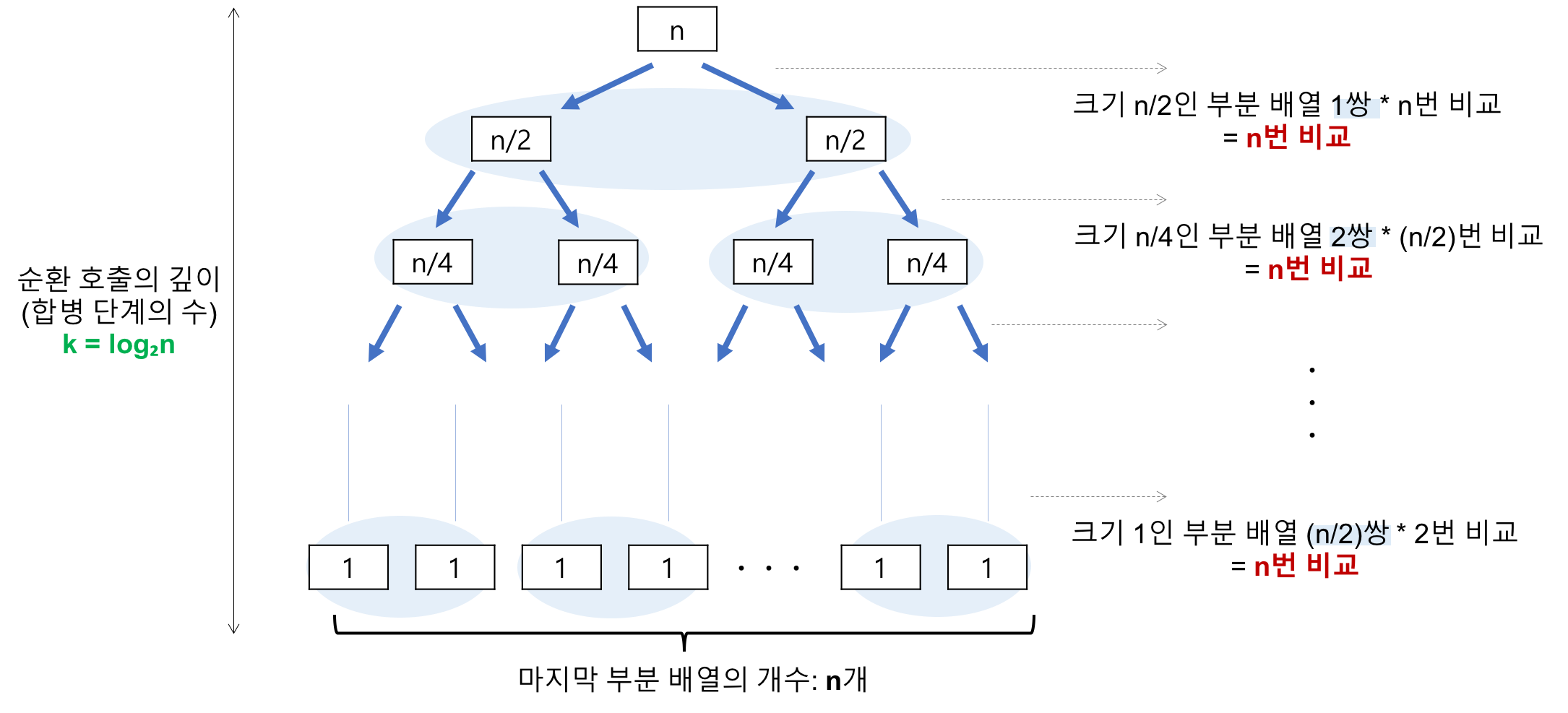
- 순환 호출의 깊이 (합병 단계의 수)
- 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
- k=log₂n
- 각 합병 단계의 비교 연산
- 크기 1인 부분 배열 2개를 합병하는 데는 최대 2번의 비교 연산이 필요하고, 부분 배열의 쌍이 4개이므로 24=8번의 비교 연산이 필요하다. 다음 단계에서는 크기 2인 부분 배열 2개를 합병하는 데 최대 4번의 비교 연산이 필요하고, 부분 배열의 쌍이 2개이므로 42=8번의 비교 연산이 필요하다. 마지막 단계에서는 크기 4인 부분 배열 2개를 합병하는 데는 최대 8번의 비교 연산이 필요하고, 부분 배열의 쌍이 1개이므로 8*1=8번의 비교 연산이 필요하다. 이것을 일반화하면 하나의 합병 단계에서는 최대 n번의 비교 연산을 수행함을 알 수 있다.
- 최대 n번
- 순환 호출의 깊이 만큼의 합병 단계 * 각 합병 단계의 비교 연산 = nlog₂n
- 이동 횟수
- 순환 호출의 깊이 (합병 단계의 수)
- k=log₂n
- 각 합병 단계의 이동 연산
- 임시 배열에 복사했다가 다시 가져와야 되므로 이동 연산은 총 부분 배열에 들어 있는 요소의 개수가 n인 경우, 레코드의 이동이 2n번 발생한다.
- 순환 호출의 깊이 만큼의 합병 단계 * 각 합병 단계의 이동 연산 = 2nlog₂n
- 순환 호출의 깊이 (합병 단계의 수)
- 비교 횟수
- T(n) = nlog₂n(비교) + 2nlog₂n(이동) = 3nlog₂n = O(nlog₂n)
정렬 알고리즘 시간복잡도 비교
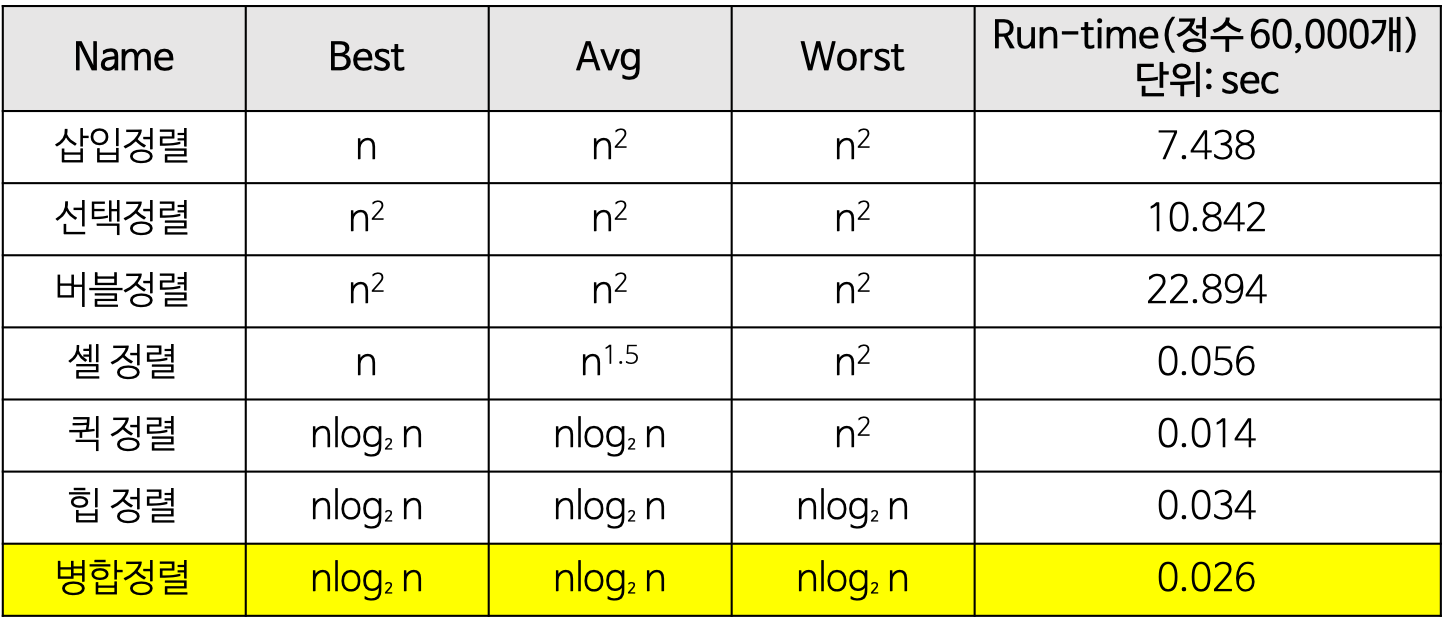
- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
관련된 Post
- 선택 정렬(selection sort): 선택 정렬(selection sort) 을 참고하시기 바랍니다.
- 삽입 정렬(insertion sort): 삽입 정렬(insertion sort) 을 참고하시기 바랍니다.
- 버블 정렬(bubble sort): 버블 정렬(bubble sort) 을 참고하시기 바랍니다.
- 셸 정렬(shell sort): 셸 정렬(shell sort) 을 참고하시기 바랍니다.
- 퀵 정렬(quick sort): 퀵 정렬(quick sort) 을 참고하시기 바랍니다.
- 힙 정렬(heap sort): 힙 정렬(heap sort) 을 참고하시기 바랍니다.


