가장 오래된 정렬 알고리즘의 하나로, 삽입정렬을 보완한 알고리즘
Goal
- 셸 정렬(shell sort) 알고리즘을 이해한다.
- 셸 정렬(shell sort) 알고리즘을 c언어로 구현한다.
- 셸 정렬(shell sort) 알고리즘의 특징
- 셸 정렬(shell sort) 알고리즘의 시간복잡도를 이해한다.
들어가기 전
- 오름차순을 기준으로 정렬한다.
셸 정렬(shell sort) 알고리즘의 개념 요약
- ‘Donald L. Shell’이라는 사람이 제안한 방법으로, 삽입정렬을 보완한 알고리즘이다.
- 삽입 정렬이 어느 정도 정렬된 배열에 대해서는 대단히 빠른 것에 착안
- 삽입 정렬의 최대 문제점: 요소들이 삽입될 때, 이웃한 위치로만 이동
- 즉, 만약 삽입되어야 할 위치가 현재 위치에서 상당히 멀리 떨어진 곳이라면 많은 이동을 해야만 제자리로 갈 수 있다.
- 삽입 정렬과 다르게 셸 정렬은 전체의 리스트를 한 번에 정렬하지 않는다.
- 과정 설명
- 먼저 정렬해야 할 리스트를 일정한 기준에 따라 분류
- 연속적이지 않은 여러 개의 부분 리스트를 생성
- 각 부분 리스트를 삽입 정렬을 이용하여 정렬
- 모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 적은 개수의 부분 리스트로 만든 후에 알고리즘을 반복
- 위의 과정을 부분 리스트의 개수가 1이 될 때까지 반복
셸 정렬(shell sort) 알고리즘의 구체적인 개념
- 정렬해야 할 리스트의 각 k번째 요소를 추출해서 부분 리스트를 만든다. 이때, k를 ‘간격(gap)’ 이라고 한다.
- 간격의 초깃값: (정렬할 값의 수)/2
- 생성된 부분 리스트의 개수는 gap과 같다.
- 각 회전마다 간격 k를 절반으로 줄인다. 즉, 각 회전이 반복될 때마다 하나의 부분 리스트에 속한 값들의 개수는 증가한다.
- 간격은 홀수로 하는 것이 좋다.
- 간격을 절반으로 줄일 때 짝수가 나오면 +1을 해서 홀수로 만든다.
- 간격 k가 1이 될 때까지 반복한다.
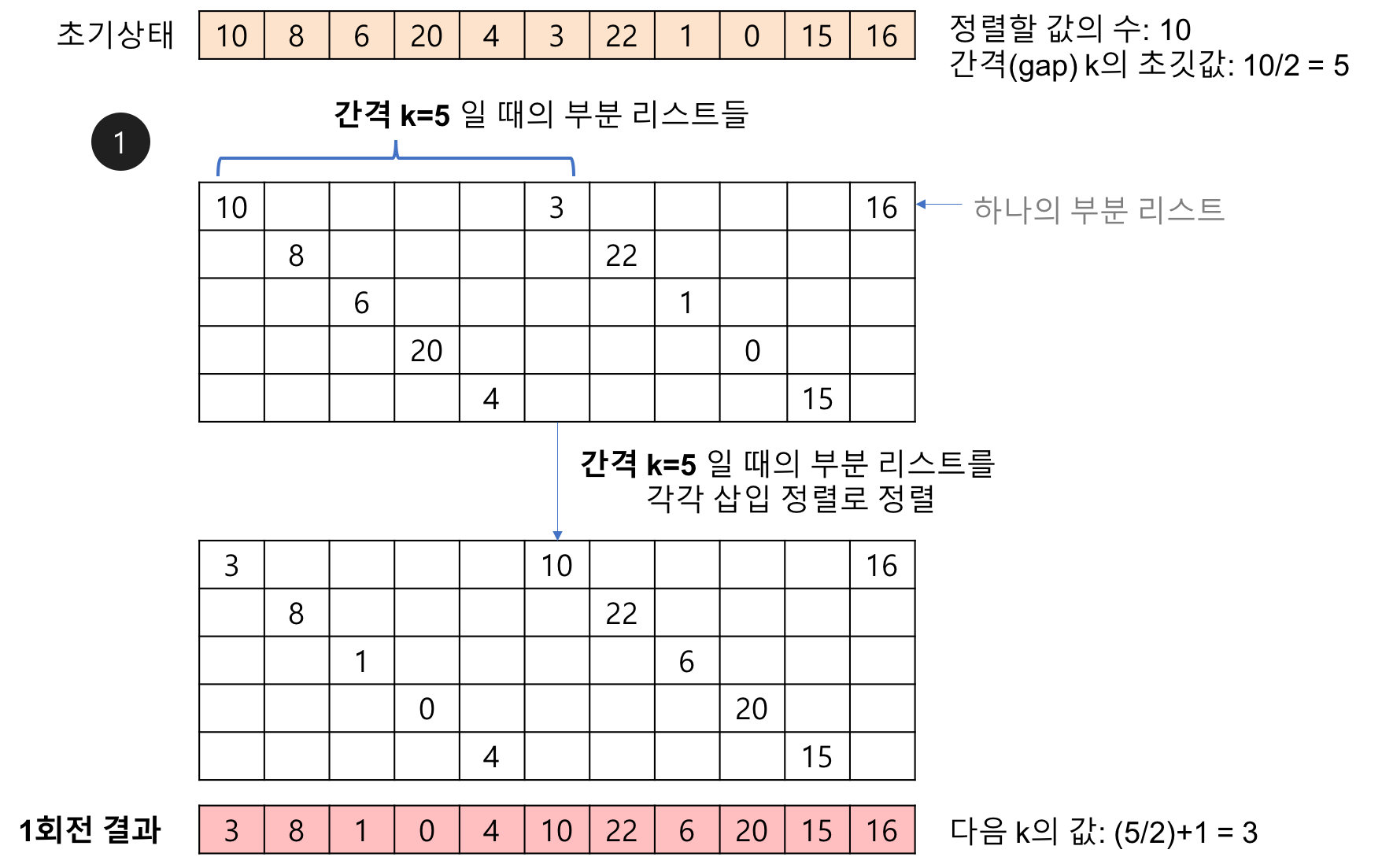
셸 정렬(shell sort) 알고리즘의 예제
-
배열에 10, 8, 6, 20, 4, 3, 22, 1, 0, 15, 16이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
-
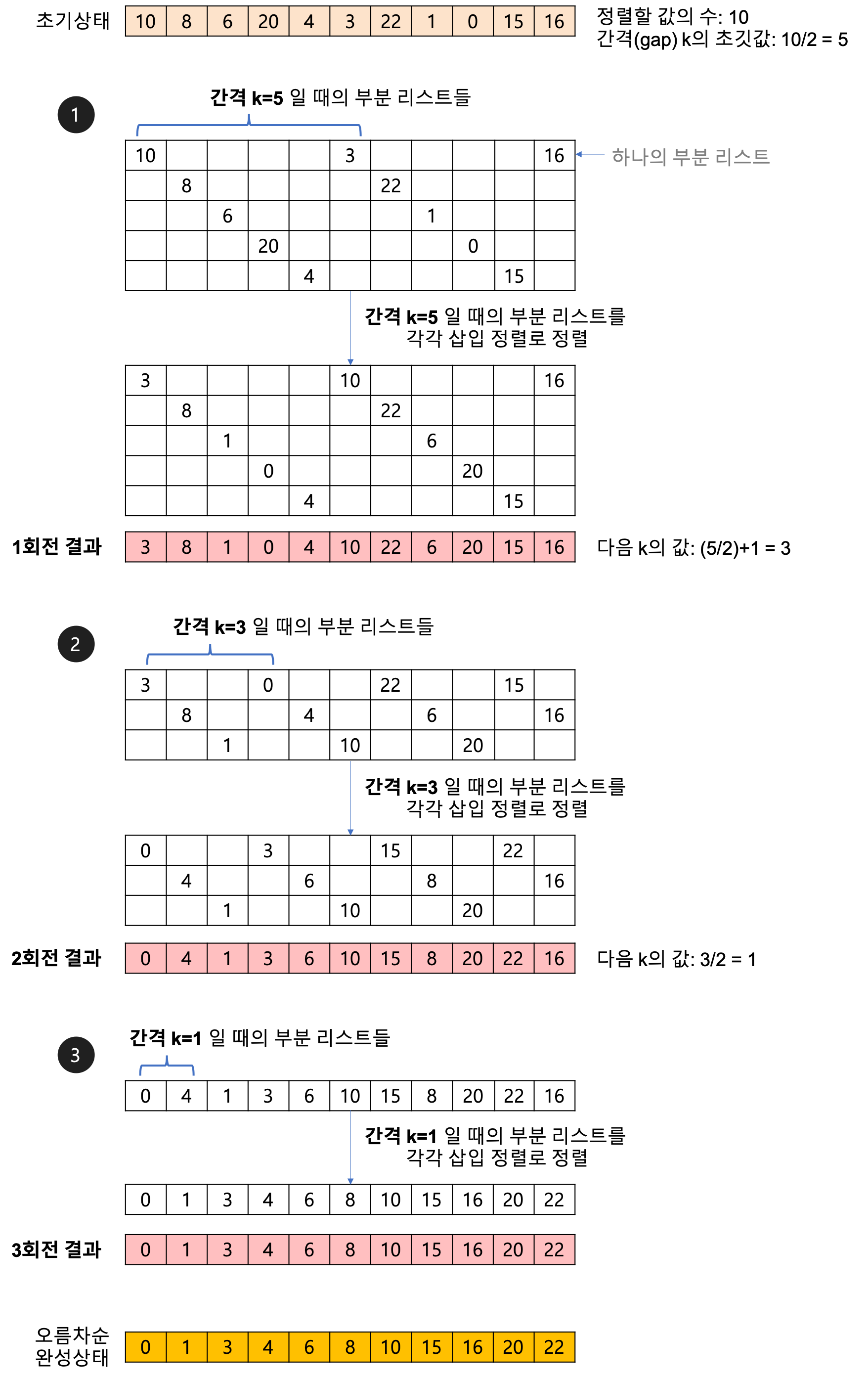
- 1회전
- 처음 간격을 (정렬할 값의 수:10)/2 = 5로 하고, 다섯 번째 요소를 추출해서 부분 리스트를 만든다. 만들어진 5개의 부분 리스트를 삽입 정렬로 정렬한다.
- 2회전
- 다음 간격은 = (5/2:짝수)+1 = 3으로 하고, 1회전 정렬한 리스트에서 세 번째 요소를 추출해서 부분 리스트를 만든다. 만들어진 3개의 부분 리스트를 삽입 정렬로 정렬한다.
- 3회전
- 다음 간격은 = (3/2) = 1으로 하고, 간격 k가 1이므로 마지막으로 정렬을 수행한다. 만들어진 1개의 부분 리스트를 삽입 정렬로 정렬한다.
셸 정렬(shell sort) c언어 코드
# include <stdio.h>
# define MAX_SIZE 10
// gap만큼 떨어진 요소들을 삽입 정렬
// 정렬의 범위는 first에서 last까지
void inc_insertion_sort(int list[], int first, int last, int gap){
int i, j, key;
for(i=first+gap; i<=last; i=i+gap){
key = list[i]; // 현재 삽입될 숫자인 i번째 정수를 key 변수로 복사
// 현재 정렬된 배열은 i-gap까지이므로 i-gap번째부터 역순으로 조사한다.
// j 값은 first 이상이어야 하고
// key 값보다 정렬된 배열에 있는 값이 크면 j번째를 j+gap번째로 이동
for(j=i-gap; j>=first && list[j]>key; j=j-gap){
list[j+gap] = list[j]; // 레코드를 gap만큼 오른쪽으로 이동
}
list[j+gap] = key;
}
}
// 셸 정렬
void shell_sort(int list[], int n){
int i, gap;
for(gap=n/2; gap>0; gap=gap/2){
if((gap%2) == 0)(
gap++; // gap을 홀수로 만든다.
)
// 부분 리스트의 개수는 gap과 같다.
for(i=0; i<gap; i++){
// 부분 리스트에 대한 삽입 정렬 수행
inc_insertion_sort(list, i, n-1, gap);
}
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {10, 8, 6, 20, 4, 3, 22, 1, 0, 15, 16};
// 셸 정렬 수행
shell_sort(list, n);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
셸 정렬(shell sort) 알고리즘의 특징
- 장점
- 연속적이지 않은 부분 리스트에서 자료의 교환이 일어나면 더 큰 거리를 이동한다. 따라서 교환되는 요소들이 삽입 정렬보다는 최종 위치에 있을 가능성이 높아진다.
- 부분 리스트는 어느 정도 정렬이 된 상태이기 때문에 부분 리스트의 개수가 1이 되게 되면 셸 정렬은 기본적으로 삽입 정렬을 수행하는 것이지만 삽입 정렬보다 더욱 빠르게 수행된다.
- 알고리즘이 간단하여 프로그램으로 쉽게 구현할 수 있다.
셸 정렬(shell sort)의 시간복잡도
시간복잡도를 계산한다면
- 평균: T(n) = O(n^1.5)
- 최악의 경우: T(n) = O(n^2)
정렬 알고리즘 시간복잡도 비교

관련된 Post
- 선택 정렬(selection sort): 선택 정렬(selection sort) 을 참고하시기 바랍니다.
- 삽입 정렬(insertion sort): 삽입 정렬(insertion sort) 을 참고하시기 바랍니다.
- 버블 정렬(bubble sort): 버블 정렬(bubble sort) 을 참고하시기 바랍니다.
- 합병 정렬(merge sort): 합병 정렬(merge sort) 을 참고하시기 바랍니다.
- 퀵 정렬(quick sort): 퀵 정렬(quick sort) 을 참고하시기 바랍니다.
- 힙 정렬(heap sort): 힙 정렬(heap sort) 을 참고하시기 바랍니다.


