서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
Goal
- 버블 정렬(bubble sort) 알고리즘을 이해한다.
- 버블 정렬(bubble sort) 알고리즘을 c언어로 구현한다.
- 버블 정렬(bubble sort) 알고리즘의 특징
- 버블 정렬(bubble sort) 알고리즘의 시간복잡도를 이해한다.
들어가기 전
- 오름차순을 기준으로 정렬한다.
버블 정렬(bubble sort) 알고리즘의 개념 요약
- 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
- 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.
- 선택 정렬과 기본 개념이 유사하다.
버블 정렬(bubble sort) 알고리즘의 구체적인 개념
- 버블 정렬은 첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬한다.
- 1회전을 수행하고 나면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 자료까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
버블 정렬(bubble sort) 알고리즘의 예제
-
배열에 7, 4, 5, 1, 3이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
-
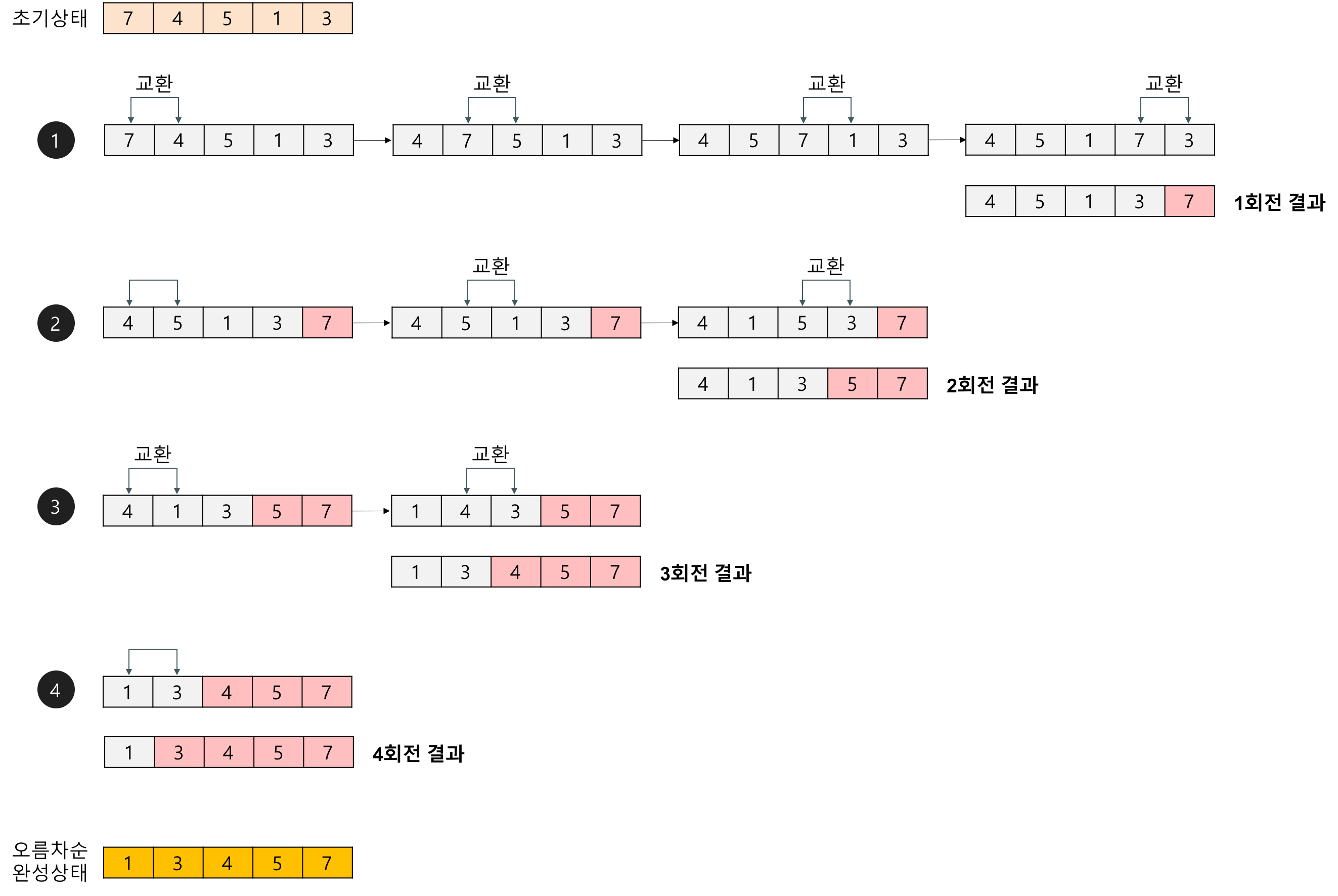
- 1회전
- 첫 번째 자료 7을 두 번째 자료 4와 비교하여 교환하고, 두 번째의 7과 세 번째의 5를 비교하여 교환하고, 세 번째의 7과 네 번째의 1을 비교하여 교환하고, 네 번째의 7과 다섯 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 네 번 비교한다. 그리고 가장 큰 자료가 맨 끝으로 이동하므로 다음 회전에서는 맨 끝에 있는 자료는 비교할 필요가 없다.
- 2회전
- 첫 번째의 4을 두 번째 5와 비교하여 교환하지 않고, 두 번째의 5와 세 번째의 1을 비교하여 교환하고, 세 번째의 5와 네 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 세 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 두 번째에 놓인다.
- 3회전
- 첫 번째의 4를 두 번째 1과 비교하여 교환하고, 두 번째의 4와 세 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 두 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 세 번째에 놓인다.
- 4회전
- 첫 번째의 1과 두 번째의 3을 비교하여 교환하지 않는다.
버블 정렬(bubble sort) c언어 코드
# include <stdio.h>
# define MAX_SIZE 5
// 버블 정렬
void bubble_sort(int list[], int n){
int i, j, temp;
for(i=n-1; i>0; i--){
// 0 ~ (i-1)까지 반복
for(j=0; j<i; j++){
// j번째와 j+1번째의 요소가 크기 순이 아니면 교환
if(list[j]<list[j+1]){
temp = list[j];
list[j] = list[j+1];
list[j+1] = temp;
}
}
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {7, 4, 5, 1, 3};
// 버블 정렬 수행
bubble_sort(list, n);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
버블 정렬(bubble sort) 알고리즘의 특징
- 장점
- 구현이 매우 간단하다.
- 단점
- 순서에 맞지 않은 요소를 인접한 요소와 교환한다.
- 하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열에서 모든 다른 요소들과 교환되어야 한다.
- 특히 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어난다.
- 일반적으로 자료의 교환 작업(SWAP)이 자료의 이동 작업(MOVE)보다 더 복잡하기 때문에 버블 정렬은 단순성에도 불구하고 거의 쓰이지 않는다.
버블 정렬(bubble sort)의 시간복잡도
시간복잡도를 계산한다면
- 비교 횟수
- 최상, 평균, 최악 모두 일정
- n-1, n-2, … , 2, 1 번 = n(n-1)/2
- 교환 횟수
- 입력 자료가 역순으로 정렬되어 있는 최악의 경우, 한 번 교환하기 위하여 3번의 이동(SWAP 함수의 작업)이 필요하므로 (비교 횟수 * 3) 번 = 3n(n-1)/2
- 입력 자료가 이미 정렬되어 있는 최상의 경우, 자료의 이동이 발생하지 않는다.
- T(n) = O(n^2)
정렬 알고리즘 시간복잡도 비교
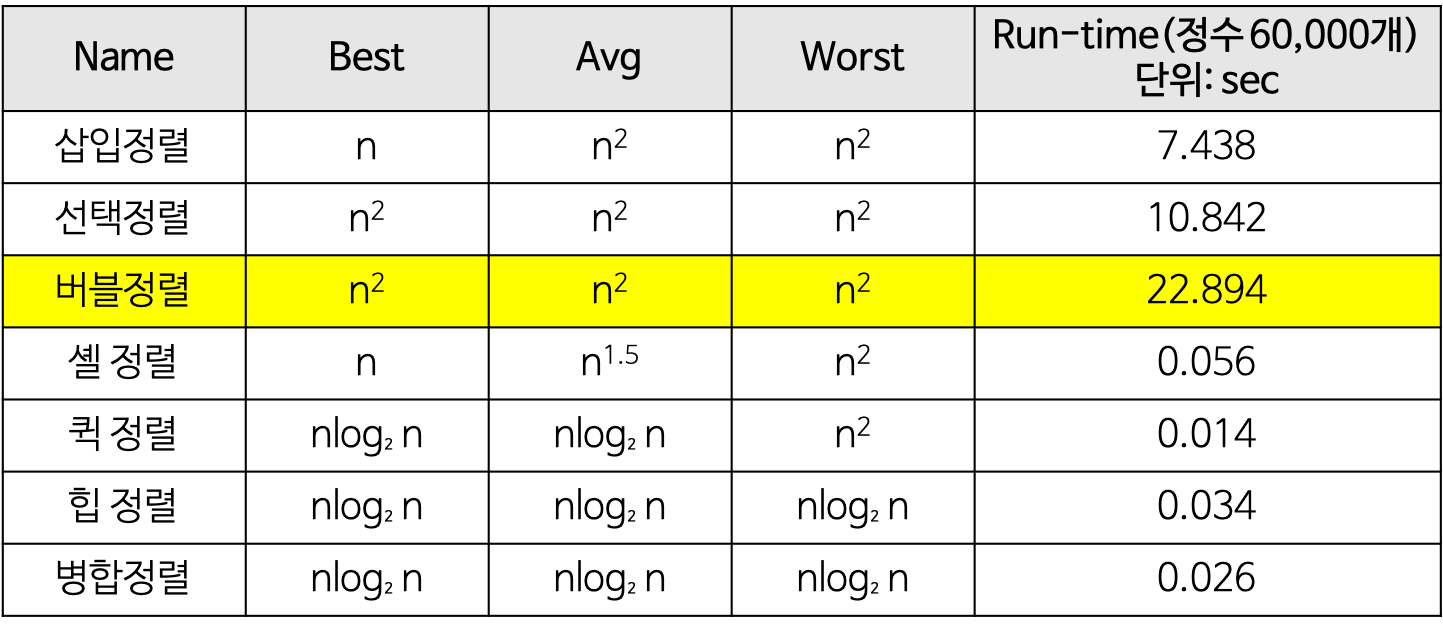
- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
관련된 Post
- 선택 정렬(selection sort): 선택 정렬(selection sort) 을 참고하시기 바랍니다.
- 삽입 정렬(insertion sort): 삽입 정렬(insertion sort) 을 참고하시기 바랍니다.
- 셸 정렬(shell sort): 셸 정렬(shell sort) 을 참고하시기 바랍니다.
- 합병 정렬(merge sort): 합병 정렬(merge sort) 을 참고하시기 바랍니다.
- 퀵 정렬(quick sort): 퀵 정렬(quick sort) 을 참고하시기 바랍니다.
- 힙 정렬(heap sort): 힙 정렬(heap sort) 을 참고하시기 바랍니다.


