위상 정렬을 이용하여 관련된 알고리즘 문제를 해결할 수 있다
Goal
- 위상 정렬(Topological Sort)이란
- 위상 정렬(Topological Sort)의 특징
- 위상 정렬(Topological Sort)과 관련된 예시
위상 정렬(Topological Sort)이란
어떤 일을 하는 순서를 찾는 알고리즘이다.
- 즉, 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것
위상 정렬(Topological Sort)의 특징
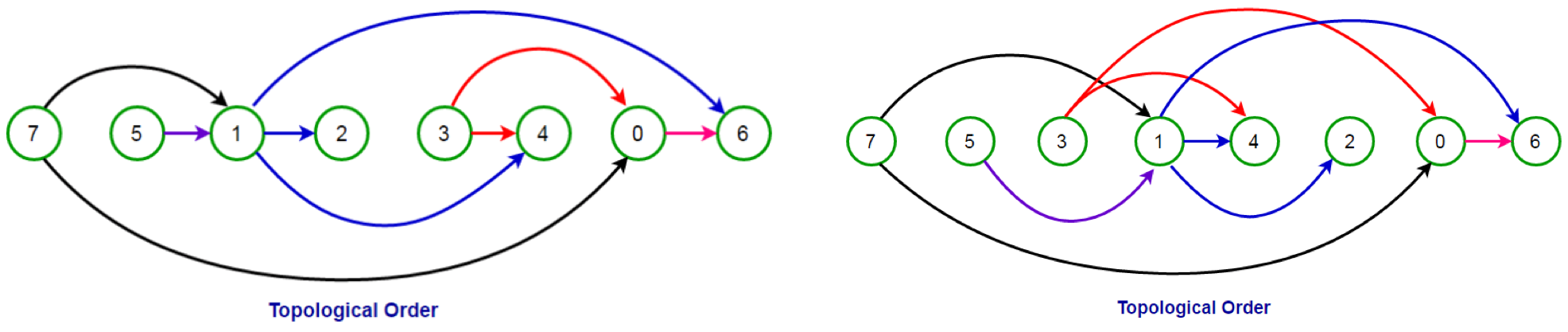
- 하나의 방향 그래프에는 여러 위상 정렬이 가능하다.
- 위상 정렬의 과정에서 선택되는 정점의 순서를 위상 순서(Topological Order)라 한다.
- 위상 정렬의 과정에서 그래프에 남아 있는 정점 중에 진입 차수가 0인 정점이 없다면, 위상 정렬 알고리즘은 중단되고 이러한 그래프로 표현된 문제는 실행이 불가능한 문제가 된다.
위상 정렬(Topological Sort)을 이용한 기본적인 해결 방법

- 진입 차수가 0인 정점(즉, 들어오는 간선의 수가 0)을 선택
- 진입 차수가 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방하다.
- 초기에 간선의 수가 0인 모든 정점을 큐에 삽입
- 선택된 정점과 여기에 부속된 모든 간선을 삭제
- 선택된 정점을 큐에서 삭제
- 선택된 정점에 부속된 모든 간선에 대해 간선의 수를 감소
- 위의 과정을 반복해서 모든 정점이 선택, 삭제되면 알고리즘 종료
위상 정렬(Topological Sort)과 관련된 예시
- 각각의 작업이 완료되어야만 끝나는 프로젝트
- 선수 과목
- 큐를 이용한 위상 정렬
- 우선순위 큐를 이용한 위상 정렬
- 여러 위상 순서 중 가장 짧게 걸리는 위상 정렬 방법 구하기
위상 정렬(Topological Sort) JAVA 코드
관련 문제: 백준 2252번
// 일부 학생들의 키를 비교한 결과가 주어졌을 때, 줄을 세우는 프로그램
public class Main {
static int N; // 그래프 정점의 수
static int M; // 간선의 수
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
N = scanner.nextInt();
M = scanner.nextInt();
int[] cntOfLink = new int[N + 1]; // 간선의 수에 대한 배열
// 가중치가 없는 그래프(인접 리스트 이용)
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
for (int i = 0; i < N + 1; i++) {
graph.add(new ArrayList<Integer>());
}
// 단방향 연결 설정
for (int i = 0; i < M; i++) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
graph.get(v1).add(v2);
cntOfLink[v2]++; // 후행 정점에 대한 간선의 수 증가
}
// 위상 정렬 (A B: A가 B앞에 선다. A가 선행)
topologicalSort(graph, cntOfLink);
}
/**
* 위상 정렬
*/
static void topologicalSort(ArrayList<ArrayList<Integer>> graph, int[] cntOfLink) {
Queue<Integer> queue = new LinkedList();
// 초기: 선행 정점을 가지지 않는 정점을 큐에 삽입
for (int i = 1; i < N + 1; i++) {
if (cntOfLink[i] == 0) { // 해당 정점의 간선의 수가 0이면
queue.add(i);
}
}
// 정점의 수 만큼 반복
for (int i = 0; i < N; i++) {
int v = queue.remove(); // 1. 큐에서 정점 추출
System.out.print(v + " "); // 정점 출력
// 2. 해당 정점과 연결된 모든 정점에 대해
for (int nextV : graph.get(v)) {
cntOfLink[nextV]--; // 2-1. 간선의 수 감소
// 2-2. 선행 정점을 가지지 않는 정점을 큐에 삽입
if (cntOfLink[nextV] == 0) { // 해당 정점의 간선의 수가 0이면
queue.add(nextV);
}
}
}
}
}
관련된 Post
- 자료구조 그래프(Graph)에 대해 알고 싶으시면 그래프(Graph)란을 참고하시기 바랍니다.
- 자료구조 큐(Queue)에 대해 알고 싶으시면 큐(Queue)란을 참고하시기 바랍니다.