이분 그래프인지 확인할 수 있다.
Goal
- 이분 그래프(Bipartite Graph)란
- 이분 그래프(Bipartite Graph)인지 확인하는 방법
이분 그래프(Bipartite Graph)란
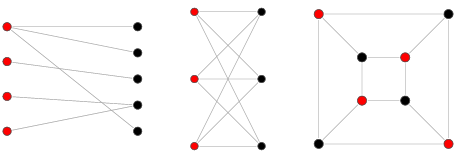 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프.
인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프.
- 즉, 그래프의 모든 정점이 두 그룹으로 나눠지고 서로 다른 그룹의 정점이 간선으로 연결되어져 있는(<=> 같은 그룹에 속한 정점끼리는 서로 인접하지 않도록 하는) 그래프를 이분 그래프라고 한다.
이분 그래프의 특징
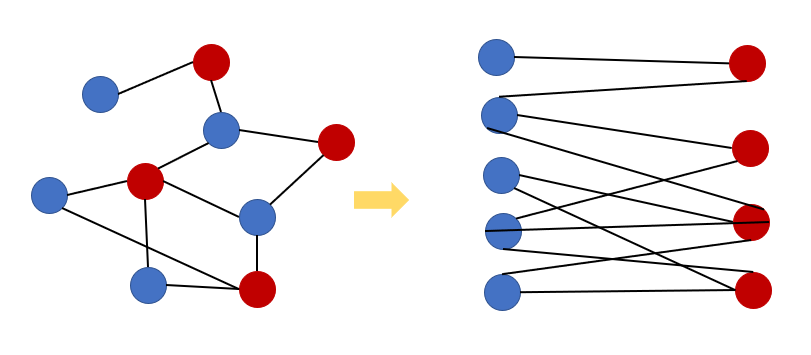
- 이분 그래프인지 확인하는 방법은 BFS, DFS 탐색을 이용하면 된다.
- 이분 그래프는 BFS를 할 때 같은 레벨의 정점끼리는 모조건 같은 색으로 칠해진다.
- 연결 성분의 개수(Connected Component)를 구하는 방법과 유사하다.
- 모든 정점을 방문하며 간선을 검사하기 때문에 시간 복잡도는 O(V+E)로 그래프 탐색 알고리즘과 같다.
이분 그래프인지 확인하는 방법
이분 그래프인지 확인하는 방법은 너비 우선 탐색(BFS), 깊이 우선 탐색(DFS)을 이용하면 된다.
- 서로 인접한 정점이 같은 색이면 이분 그래프가 아니다.
- BFS, DFS로 탐색하면서 정점을 방문할 때마다 두 가지 색 중 하나를 칠한다.
- 다음 정점을 방문하면서 자신과 인접한 정점은 자신과 다른 색으로 칠한다.
- 탐색을 진행할 때 자신과 인접한 정점의 색이 자신과 동일하면 이분 그래프가 아니다.
- BFS의 경우 정점을 방문하다가 만약 같은 레벨에서 정점을 다른 색으로 칠해야 한다면 무조건 이분 그래프가 아니다.
- 모든 정점을 다 방문했는데 위와 같은 경우가 없다면 이분 그래프이다.
- 이때 주의할 점은 연결 그래프와 비연결 그래프를 둘 다 고려 해야한다는 것이다.
- 그래프가 비연결 그래프인 경우 모든 정점에 대해서 확인하는 작업이 필요하다.
이분 그래프인지 확인하는 JAVA 코드
관련 문제: 백준 1707번
public class Main {
static Scanner scanner = new Scanner(System.in);
static ArrayList<ArrayList<Integer>> arrayLists; // 그래프
static final int RED = 1;
static final int BLUE = -1;
static int[] colors; // 색 {RED 1 or BLUE -1}
static boolean checkBipartite; // 이분 그래프인지 아닌지 확인
public static void main(String[] args) {
int testCase = scanner.nextInt(); // 테스트 케이스
while (testCase-- > 0) {
int V = scanner.nextInt(); // 정점의 개수 V (1≤V≤20,000)
int E = scanner.nextInt(); // 간선의 개수 E (1≤E≤200,000)
arrayLists = new ArrayList<>();
colors = new int[V + 1]; // 각 정점의 색을 구분
checkBipartite = true; // 초기: 이분 그래프이다.
for (int i = 0; i < V + 1; i++) {
arrayLists.add(new ArrayList<Integer>()); // 정점의 수 + 1만큼 초기화
colors[i] = 0; // 방문하지 않은 정점의 색을 0으로 초기화
}
// 양방향 그래프 연결
while (E-- > 0) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
arrayLists.get(v1).add(v2);
arrayLists.get(v2).add(v1);
}
// 이분 그래프: 같은 레벨의 꼭짓점끼리는 무조건 같은 색, 인접한 정점 사이는 다른 색
// 주의! 연결 그래프와 비연결 그래프(모든 정점을 돌면서 확인) 모두 고려!!
for (int i = 1; i < V + 1; i++) {
// 이분 그래프가 아니면 반복문 탈출
if (!checkBipartite)
break;
// 방문하지 않은 정점에 대해서 탐색 수행
if (colors[i] == 0) {
// dfs(i, RED); /* 깊이 우선 탐색 */
bfs(i, RED); /* 너비 우선 탐색 */
}
}
System.out.println(checkBipartite ? "YES" : "NO");
}
}
/* 깊이 우선 탐색 */
static void dfs(int startV, int color) {
colors[startV] = color; // 시작 정점의 색을 설정
for (int adjV : arrayLists.get(startV)) {
// 시작 정점의 색과 인접한 정점의 색이 같으면 이분 그래프가 아니다.
if (colors[adjV] == color) {
checkBipartite = false;
return;
}
// 시작 정점과 인접한 정점이 방문하지 않은 정점이면 dfs 실행
if (colors[adjV] == 0) {
// 인접한 정점을 다른 색으로 지정
dfs(adjV, -color);
}
}
}
/* 너비 우선 탐색 */
static void bfs(int startV, int color) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(startV); // root 정점을 큐에 삽입
colors[startV] = color; // root 정점 방문 표시 + 색 표시
// 큐가 비어있지 않고 이분 그래프 == ture 면 반복
while (!queue.isEmpty() && checkBipartite) {
int v = queue.poll(); // 큐에서 정점 추출
// 해당 정점과 연결된 모든 인접 정점을 방문
for (int adjV : arrayLists.get(v)) {
// 방문하지 않은 정점이면
if (colors[adjV] == 0) {
queue.offer(adjV); // 인접 정점을 큐에 삽입
colors[adjV] = colors[v] * -1; // 인접한 정점을 다른 색으로 지정
}
// 서로 인접한 정점의 색이 같은 색이면 이분 그래프가 아니다.
else if (colors[v] + colors[adjV] != 0) {
checkBipartite = false;
return;
}
}
}
}
}
관련된 Post
- 자료구조 그래프(Graph)에 대해 알고 싶으시면 그래프(Graph)란을 참고하시기 바랍니다.
- 깊이 우선 탐색(DFS, Depth-First Search): 깊이 우선 탐색(DFS)이란 을 참고하시기 바랍니다.
- 너비 우선 탐색(BFS, Breadth-First Search): 너비 우선 탐색(BFS)이란 을 참고하시기 바랍니다.